Pada saat membahas materi tentang fungsi, kita telah mempelajari bagaimana menentukan nilai fungsi f(x) di x = a.
Sebagai contoh,
Diketahui
Untuk x = -1 diperoleh f(-1) = 1. Untuk x = 1 diperoleh f(1) = 3.
Berapakah nilai f(x) untuk x = 0?
Ternyata, kita tidak dapat menentukan nilai f(x) di x = 0, sebab pembagian bilangan hanya terdefinisi jika pembagi tidak sama dengan 0. Akan tetapi, kita masih dapat mempelajari bagaimana nilai f(x) jika x mendekati 0 dengan menggunakan konsep limit.
A. PENGERTIAN DAN NOTASI LIMIT
Dalam kehidupan sehari-hari,
seringkali kita mendengar kata-kata hampir
atau mendekati. Misalnya, Egy hampir saja mencetak gol, kecepatan
motor itu mendekati 120 km/jam, dsb. Kata hampir atau mendekati dalam matematika
disebut limit.
Dalam matematika, limit merupakan nilai hampiran suatu variabel pada suatu bilangan real.
Notasi
dibaca sebagai “limit fungsi f(x) dimana x mendekati a sama dengan L”, dan diartikan sebagai “ jika x mendekati a, maka f(x) mendekati L”
Teorema :
Misalkan f suatu fungsi serta L dan
a adalah bilangan real, maka
Untuk lebih memahaminya perhatikan uraian
berikut.
B. PENGERTIAN LIMIT SECARA INTUITIF
Masalah 1.
Selidiki apakah nilai
ada atau tidak ada?. Jika ada berpakah nilainya?
Pembahasan
·
Untuk
x mendekati 3 dari kiri
Perhatikan
tabel berikut :
· Untuk x mendekati 3 dari kanan
Berdasarkan hasil perhitungan pada tabel di atas dapat disimpulkan bahwa
o Jika x mendekati 3 dari kanan, maka nilai akan mendekati 6
atau ditulis dengan notasi limit sebagai
Berdasarkan pembahasan di atas diperoleh
atau limit kiri = limit kanan,
Soal latihan 1 – (tugas BDR 1)
Selidikilah apakah nilai limit berikut ada atau tidak. Jika ada tentukan nilainya.
C. MENENTUKAN NILAI LIMIT FUNGSI
Setelah mengetahui cara mengetahui apakah suatu fungsi limitnya ada atau tidak secara intuitif, maka selanjutnya kita akan bahas bagaimana cara menentukan nilai limit suatu fungsi, khusunya limit fungsi aljabar. Namun demikian kita akan lihat dulu sifat-sifat limit sebagai berikut.
Sifat-sifat Limit Fungsi
Perhatikan bagan berikut ini.
Berikut diberikan contoh-contoh cara menyelesaikan limit fungsi aljabar.
CONTOH. 1
Tentukan nilai dari
Jawab:
Substitusikan x = 2, diperoleh
Jadi
CONTOH. 2
Tentukan nilai dari
Jawab:
Substitusikan x = 1, diperoleh
Jadi
CONTOH. 3
Tentukan nilai dari
Jawab:
Jadi
CONTOH. 4
Tentukan nilai dari
Jawab:
substitusi x = -3, diperoleh
Jadi
CONTOH 5.
Tentukan nilai dari
Substitusi x =0,
diperoleh
Jadi
Soal Latihan 2 – Tugas PTMT 1
Hitung nilai limit berikut
Selain dengan cara memfaktorkan atau
mengalikan dengan faktor sekawannya, ada cara lain untuk menentukan nilai limit
fungsi, khusunya fungsi yang sulit untuk difaktorkan atau dikalikan dengan
faktor sekawannya.
CONTOH 6.
Tentukan nilai dari
Jawab :
Jika dilakukan dengan substitusi maka
diperoleh bentuk tak tentu
CONTOH 7.
Masalah kontekstual
Sebuah bidang logam dipanaskan di bagian
tengah dan memuai sehingga mengalami pertambahan luas sebagai fungsi waktu f(t)
= 0,25 t2 + 0,5 t cm2.
Tentukan kecepatan perubahan pertambahan
luas bidang tersebut pada saat t = 5 menit.
Jawaban:
Kecepatan perubahan pertambahan luas adalah besar pertambahan luas dibandingkan dengan besar selisih waktu dan dapat dirumuskan sebagai
Kecepatan perubahan pertambahan luas bidang tersebut pada saat t = 5 menit adalah
CONTOH 8.
tentukan nilai dari
Jawab :
CONTOH 9.
tentukan
Jawab.
Soal Latihan 3 – Tugas BDR 3










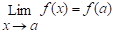


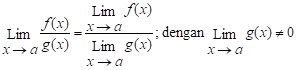















































Tidak ada komentar:
Posting Komentar