Dalam kehidupan sehari-hari seringkali kita berhadapan dengan suatu kejadian yang belum pasti atau suatu kemungkinan. Nilai kejadian yang belum pasti atau nilai kemungkinan dari suatu kejadian disebut dengan peluang (Probabilitas). Peluang merupakan nilai perbandingan antara banyaknya suatu kejadian dengan nilai seluruh kejadian yang mungkin terjadi dari suatu peristiwa atau percobaan. Seluruh kejadian yang mungkin terjadi dari suatu peristiwa atau percobaan disebut sebagai Ruang Sampel.
Jika X suatu kejadian dan S ruang sampel maka Peluang kejadian X adalah
dengan n(x) banyaknya kejadian X dan n(S) banyaknya anggota ruang sampel.
Nilai peluang suatu kejadian berkisar antara 0 dan 1, oleh karena itu pada kejadian X berlaku :
- 0 < P(X) < 1
- P(X)+P(bukan X) = 1
PELUANG KEJADIAN TUNGGAL
Peluang kejadian tunggal merupakan peluang dimana kejadian yang terjadi hanya terdiri dari satu kejadian saja. Untuk memahami tentang Peluang Kejadian Tunggal perhatikan tabel berikut.
Contoh 1.
Pada pelemparan 2 koin secara bersamaan sebanyak 1 kali, tentukan Peluang munculnya satu gambar.
Penyelesaian
Pada pelemparan 2 koin sebanyak 1 kali, maka ruang sampelnya adalah S ={AA, AG, GA, GG} dan n(S) = 4
Misalkan X adalah kejadian muncul satu gambar, maka X = {AG, GA} dan n(X) = 2
Sehingga Peluang kejadian muncul satu gambar adalah
Contoh 2.
Pada pelemparan 3 koin secara bersamaan sebanyak 1 kali, tentukan Peluang munculnya dua gambar.
Penyelesaian
Pada pelemparan 3 koin sebanyak 1 kali, maka ruang sampelnya adalah S ={AAA, AAG, AGA, AGG, GAA, GAG, GGA, GGG} dan n(S) = 8
Misalkan X adalah kejadian muncul dua gambar, maka X = {AGG, GAG, GGA} dan n(X) = 3
Sehingga Peluang kejadian muncul dua gambar adalah
Soal Latihan 1
- Apakah pada pelemparan 2 koin secara bersamaan sebanyak 1 kali memiliki ruang sampel yang sama dengan pelemparan 1 koin sebanyak 2 kali? Untuk menjawabnya silahkan lakukan percobaan melempar 2 koin sebanyak 1 kali dan melempar 1 koin sebanyak 1 kali. Lalu catat semua kemungkinan yang dapat terjadi dari masing-masing percobaan tersebut.
- Pada pelemparan 2 buah koin secara bersamaan, tentukan Peluang munculnya paling sedikit satu angka.
- Pada pelemparan 3 koin secara bersamaan sebanyak 1 kali, tentukan peluang munculnya paling sedikit 2 angka.
Selanjutnya perhatikan tabel berikut
Pada peristiwa pelemparan 2 dadu, maka ruang sampelnya disajikan pada tabel berikut :
Kejadiannya adalah sebagai berikut:
pada dadu 1 muncul mata 1 dan dadu 2 muncul mata 1 ditulis (1,1), atau
pada dadu 1 muncul mata 1 dan dadu 2 muncul mata 2 ditulis (1,2), atau
pada dadu 1 muncul mata 1 dan dadu 2 muncul mata 3 ditulis (1,3), atau
dan seterusnya …….
pada dadu 1 muncul mata 6 dan dadu 2 muncul mata 4 ditulis (6,4), atau
pada dadu 1 muncul mata 6 dan dadu 2 muncul mata 5 ditulis (6,5), atau
pada dadu 1 muncul mata 6 dan dadu 2 muncul mata 6 ditulis (6,6).
sehingga
S = {(1,1),(1,2),(1,3), …., (6,4), (6,5), (6,6)} dan n(S) = 36
Contoh 3.
Pada pelemparan 1 dadu sebanyak 1 kali, tentukan Peluang munculnya mata dadu bilangan genap.
Penyelesaian
Pada pelemparan 1 dadu sebanyak 1 kali, maka ruang sampelnya adalah S ={1, 2, 3, 4, 5, 6} dan n(S) = 6
Misalkan X adalah kejadian muncul mata dadu bilangan genap, maka X = {2,4,6} dan n(X) = 3
Sehingga Peluang kejadian muncul mata dadu bilangan genap adalah
Contoh 4.
Pada pelemparan 2 dadu sebanyak 1 kali secara bersamaan, tentukan Peluang munculnya mata dadu berjumlah 8
Penyelesaian
Pada pelemparan 2 dadu sebanyak 1 kali, maka ruang sampelnya disajikan pada tabel berikut :
dan n(S) =36.
Misalkan X adalah kejadian munculnya mata dadu berjumlah 8, maka X = { (2,6), (3,5),(4,4),(5,3),(6,2) } dan n(X) = 5
Sehingga Peluang kejadian muncul mata dadu berjumlah 8 adalah
Soal latihan 2
- Pada pelemparan sebuah dadu sebanyak 1 kali secara bersamaan, tentukan Peluang munculnya mata dadu lebih dari 2.
- Pada pelemparan 2 dadu sebanyak 1 kali secara bersamaan, tentukan Peluang muncul mata dadu dengan jumlah kurang dari 6



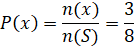





Tidak ada komentar:
Posting Komentar